Statistical Significance Explained
- Slaven Bogdanovic
- Nov 3, 2021
- 8 min read
On the Example of A/B Testing
We frequently hear that a result is "statistically significant." But, what does that mean? Can we explain it in simple language to stakeholders who do not have research or statistical background?
When we compare products or concepts, we are often faced with the question of the statistical significance of the results. This post aims to provide a starting point for the conceptual understanding of statistical significance, using the example of widespread A/B testing.
To find out which product to launch – A or B, we might ask people to estimate how much they like products A and B. Typically, we use 5 points scale where 1 stands for "Dislike it very much" and 5 for "Like it very much"[1]. Imagine that for the product A we get an average score of 2.9, and that for the product B we get 3.1. We see that B performed a bit better, but is the difference striking enough to really call it a difference in performance? More precisely put, can we assume that the difference also exists in the population that we are actually interested in (e.g. our targeted customers), and is not just a fluke in our sample? To extrapolate the conclusions beyond the specific sample, we have to apply statistical inference.
[1] This type of scale is called the Likert scale based on the psychologist who invented it
Key metrics: What do I need?
Purchase intention: „How likely are you to purchase this product during your next purchase? 1 - not likely at all, 2 - not likely, 3 - not sure, 4 - likely, 5 - very likely“
Overall likeability: „Overall, how do you like this product? "1 – dislike it very much, 2 – dislike it, 3 – Neither like it nor dislike it. 4 – like it very much, 5 – like it“
Performance on the image attributes: „To which extent do you agree with the following ways to describe this product? -High quality/Professional/Technology advanced etc. 1 - Completely disagree, 2 – Disagree, 3 - Neither agree nor disagree, 4 – Agree, 5 – Completely agree.“
Direct comparison: „Which product do you like better?“, „Which of the products would you choose to buy?“
The main concepts: What should I know?
What is A/B testing?
To predict future success of products, services, or concepts before launching them (but also to compare the performance of the existing ones), we can do a survey to compare them on various metrics (overall likeability, purchase intention, brand image, etc.). This type of study is commonly known as A/B testing, and it’s one of the basics of market research.
Survey design types
Two typical survey designs for A/B testing are monadic and sequential monadic. With the monadic A/B test, you show only one concept/product/service per group of people and then compare the groups' results. With sequential monadic, you offer more than one concept/product/service to the same group of people in randomized order. Each of the designs has its advantages. Sequential monadic is more sample-efficient and offers the possibility of direct comparison, while monadic leaves space for more questions (without exhausting the respondent).
The interpretation of the outcome: How should we read it?
What is statistical inference?
In large majority of cases, our interest is not limited to the sample that we used in our survey. The sample we are doing the study on is just a means to learn something about the population. Population is any group of people of interest to us, typically our current and potential customers. Since the testing of the whole population is not practical (or even possible in most cases), we use statistical inference based on the sample to make assumptions about the population.
Fundamental prerequisites for statistical inference are that the sample is random and that it is large enough. For more information on sampling, go to our posts dedicated to sample randomness and sample size. In short, randomness means that every member of the population has an equal chance of ending up in our sample. This is important because it means that there is no bias stemming from members with specific characteristics being more likely to be included in the sample, skewing the results. The adequate sample size depends on the variability of the metric that we are interested in, and the amount of imprecision we are willing to tolerate. The rule of thumb says not to go under 30 respondents per cell (for example, if we want to contrast the performance of men and women, we should have at least 30 men and 30 women).
Let's get back to our example. Recall that we have products A and B and their respective average scores of 2.9 and 3.1 on the 5pt likeability scale. Imagine one scenario in which those average scores are mostly comprised out of 3s, with just a couple of 2s and 4s. Now, image another scenario, in which the identical scores are made up mostly out of 1s and 5s. Do you think that those two scenarios are comparable? If you said – no, you had a good intuition. In the first scenario, we have means that describe (or "fit ") individual data points more precisely than in the second scenario.
Standard deviation
So, mean by itself is not sufficient to fully describe our data. We need some other complementary measure that informs us about the variability of our data. One of the best-known measures of variability is the standard deviation:
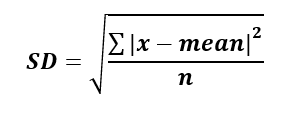
While we do understand that some people might be weary of math, we think understanding what standard deviation is is worth the effort, since it’s one of the pillars of many data analysis techniques. It is simply a measure summarizing distance (dispersion) of the data points from the mean. Some of the data points are above the mean, and others are below the mean. A simple addition of all the distances would yield zero (since the positive and negative deviations from the mean would cancel out). To avoid that, we square the distances to shift them all above zero. After that, the result is divided by sample size, N[2], and finally a square root is taken to reverse the squaring we did. In our first scenario (where people mostly answered with 3s along with some 2s and 4s) the standard deviation is smaller than in the second scenario (where we have a lot of 1s and 5s). By considering the standard deviation along with the mean, we get a much more comprehensive picture of our data.
[2] You will often see formulas where the denominator is N-1, instead of N. We opted for the formula with N, since the rationale behind using N-1 instead is quite complex, and not crucial for understanding the bigger picture (and the result is basically the same anyway)
The t-test for comparing the means
Ok, so how does standard deviation help us compare the means? When we compare means with smaller standard deviations, we can be more confident that the difference we got in our example also exists in the population. The test that we use for the comparison of two means is called the t-test. As the input values for calculating the t-test, we use means, standard deviations, and the sample size. The result of the t-test is called the t-score. T-score is higher if we have a larger difference between the means, smaller standard deviations of the means, and larger samples in the groups whose means we are comparing. In the final step, we look up the probability[2] that we could have gotten a t-score of that particular size or higher if the difference between the means actually didn’t exist. The higher our t-score is, the lower the probability that we got it fortuitously. Try out our t-test calculator:
The most commonly used boundary for proclaiming a significant result is 0.05. We say that the result is significant „at the level of 0.05“. It means that there is probability of 0.05 that we got a t-score that high by a fluke in our sample, and that in reality there is no difference in the population. So, with a result significant at the 0.05 level, we still have a 5% chance of making a mistake or declaring that there is a difference when in reality there is none. However, statisticians have somehow agreed that we can live with that. Technically, you could use any significance level you wanted, but there are a several standardly used ones. Besides 0.05, analysts often use a more rigorous 0.01 level, and a more relaxed 0.1 level.
[2] We can do that because we know that t-score follows the t-distribution of probability (which is similar to the normal distribution, although the explanation of their differences is beyond the scope of this post). From the t-distribution we can read the probability of each value of t-score.
Multiple comparisons
With 0.05 significance level, we can (roughly) also say that we are 0.95 certain that we are right. But, if we are contrasting more than two test materials, things get a bit more complicated. If we had three products, A, B, and C, to figure out which is the best we would have to compare A vs. B, B vs. C, and A vs. C. In that case, we are not 0.95 certain anymore, but 0.95 x 0.95 x 0.95 = 0.86. To prevent this inflation of uncertainty, we typically use Bonferroni correction. Unfortunately, this uncertainty-inflation effect is often neglected in business analytics, leading to erroneous conclusions. On the other hand, Bonferroni correction has its disadvantages as well - it is very conservative, meaning that it can potentially suppresses actual differences. If we want to be more precise in our analysis, in the case of multiple comparison we should go for the analysis of variance (ANOVA). However, since ANOVA requires more processing than the usually used t-test, it is not encountered less in the business data analysis.
Survey design also has implications for the analysis. If we do monadic testing (one group evaluates A, and another group evaluates B), we should apply an independent samples t-test. On the other hand, if we do a sequential monadic testing (same group evaluates both A and B), we need to use dependent samples t-test. This fact is, sadly, also frequently neglected in practice. Analysts commonly use independent samples tests for both scenarios, likely because the independent samples t-test is more often integrated into software for crosstabulation. Using an independent samples t-test to analyze data obtained through sequential monadic design increases the probability of falsely proclaiming the difference exists when they, in fact, do not.
Comparing proportions with the z-test
For comparison of proportions of the answers, we use the z-test. A prerequisite for the z-test is that groups that we compare are independent, i.e., obtained through monadic testing. Try our z-test calculator:
If we have dependent measures collected by sequential monadic design, we should go for the McNemar test. McNemar is even less common in business practice than the dependent samples t-test. However, you should be aware that by using z-tests instead of McNemar tests for analyzing the results obtained through sequential monadic design, you are overestimating the significance of the differences between the percentages you are comparing.
Key take-aways: How can I use it?
We commonly use A/B tests as a tool for quickly detecting the best-performing option. However, you do not have to stop here. If you dig a little deeper into the data, you can figure out the reasons for the difference. Those learnings can improve your future development. Using driver analysis, you can find the product attributes (e.g., brand image, product characteristics, etc.) that are most related to overall likeability or another overall performance metric.



Comments